NETWORKS
Perhaps the single most useful application of graphs comes from the study of networks. The interstate highway system is an example of a network: given any city on the system, it is possible to find a route or path from that city to any other city on the system. Formally, as this example suggests, a network is a graph in which a path can be found between any two vertices.
NETWORK
 A network is a connected graph.

EXAMPLE 1
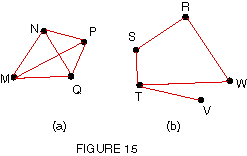
The graph in Figure 14(a) is a network. The one in Figure 14(b) is not, since there is no path between M and P, for example.
   A cycle is a route that goes from one vertex back to the same vertex without passing along any edge more than once. For example, the graph in Figure 15(a) has five cycles: PNQP, NMPN, MQNM, QPMQ, and PNMQP. The graph in Figure 15(b) has only one cycle, WRSTW.
   Graph theory is used to produce the minimum total cost when designing a network, such as a pipeline. For example, in the graph in Figure 15(b), the connection between W and T isn't really necessary since T can be reached from W by going through R and S. (Alternatively, the connection between W and R could be omitted, with W reached from R by going though T and S.) A network with no cycles is called a tree. In a tree, there is only one path between any two vertices.

EXAMPLE 2

The graph in Figure 15(b) is not a tree because of the cycle WRSTW. However, the network becomes a tree if edge WR or edge WT is omitted, as seen in Figure 16.

   A tree that contains all the vertices of a network is called a spanning tree. Think of a spanning tree as a sort of "skeleton" for the graph: the spanning tree includes all the vertices of the graph:; any edges that are not really necessary for each vertex to be reachable from al other vertices are omitted.

EXAMPLE 3

Find a spanning tree for the network in Figure 17.
   This network contains several cycles, such as ACDEA, ACDFEA, AEFBA, ACDFBA, and so on. A spanning tree must contain no cycles, so it is necessary to remove at least one edge from each cycle. Two possible spanning trees are shown in Figure 18. Many others are possible.
   In an application, a length or cost is assigned to each edge of a network. For example, lengths might be assigned when designing a new microwave relay network, and costs might be assigned for a pipeline project where some parts go through relatively flat land but other parts involve expensive construction through mountains. In a network, a spanning tree for which the sum of numbers assigned to edges is a minimum is called a minimum spanning tree.
 

EXAMPLE 4
Find the minimum spanning tree for the network in Figure 19.
   Only four spanning trees are possible for this network; they are shown in Figure 20. In the second spanning tree, the sum of the edge numbers is 30, the smallest of the four sums. This makes BCDA the minimum spanning tree.
   The minimum spanning tree for Example 4 was found by considering all possible spanning trees. This approach would be much too time-consuming in practice. Instead, we find the minimum spanning tree for a network by using the following procedure.
FINDING THE MINIMUM SPANNING TREE
 To find a minimum spanning tree for a network with numbers assigned to each edge:
  1. Find the edge with the smallest number (if more than one edge has this number, choose any one of them).
  2. Consider any edge with the next smallest number. If it would form a cycle with the edges already chosen, reject it; otherwise choose it.
  3. Repeat Step 2 until the number of edges is one less than the number of vertices.

    Since several edges might have equal numbers, there may be more than one minimum spanning tree.

EXAMPLE 5
A company has branches in Washington D.C., Charlotte, Nashville, Louisville, and Kansas City. The company wishes to build a private communications line between all these branches and Chicago headquarters. Find the line of minimum distances that will connect all the cities.
   The first step is to draw a network showing all possible connections and the corresponding distances. this is done in Figure 21. (The numbers represent straight line distances, but it is not convenient to draw all the edges as straight lines.)
To find a minimum spanning tree, start with the edge with the smallest number,
Louisville-Nashville 174
 
The next smallest number is associated with the edge
 
Chicago-Louisville 297
  Next, use the edge
 
Washington-Charlotte 382
  Now use
 
Charlotte-Nashville 421
  The next smaller number is Louisville-Charlotte, at 456 miles, but this edge would complete a cycle, so it cannot be used. The next usable edge is
 
Louisville-Kansas City 513
  The minimum spanning tree is shown in Figure 22. The length of this minimum spanning tree is
 
513 + 297 + 174 + 421 + 382 = 1787 miles.
  Any other spanning tree would produce a greater total mileage.
   
 
 

Exercises

Identify all cycles in the following networks
1. 2. 3. 4.
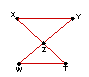Find all spanning trees for each network.
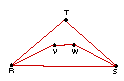
5. 6.
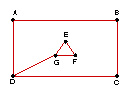7. 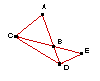8.
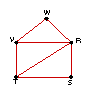Find a minimum spanning tree for each network.
9. 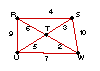10.
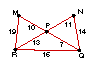11. 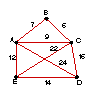12.
 
 

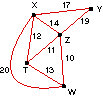Applications

BUSINESS AND ECONOMICS
Minimum Cost
 13. Find the cost for the pipeline below, in which the numbers represent costs in suitable units.
Minimum Cost 14. Find the minimum cost for the internal telephone system represented below, in which the numbers represent costs in appropriate units.
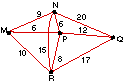  SOCIAL SCIENCES
Distances Between Cities 15. The distances between cities A, B, C, D, and E are given in the following mileage chart.
  A B C D E
A   168 352 152 317
B 168   177 172 296
C 352 177   235 152
D 152 172 235   164
E 317 296 152 164  
Find the minimum spanning tree for this network of cities.
Distances Between Cities 16. The distances between cities R, S, T, V, W, and X are given in the following mileage chart.
  R S T V W X
R   106 154 194 202 91
S 106   208 274 301 137
T 154 205   82 116 201
V 194 274 82   192 195
W 202 301 116 192   274
X 91 137 201 195 274  
Find the minimum spanning tree for this network of cities.



Copyright © 1995-2012, Pearson Education, Inc.