COMMUNICATION DIGRAPHS
In our study of dominance digraphs, we found that the associated matrix was asymmetric; that is, if the entry in row i and column j was a 1, say, then the entry in row j and column i had to be 0. With communication digraphs, however, the associated matrices are symmetric. The symmetry follows from the nature of communication; if A can communicate with B, then (normally) B can also communicate with A. Communication digraphs arise in studies of highway networks, pipelines, airline routes, and telephone links between cities.

   A communication digraph has the following properties.

COMMUNICATION DIGRAPH
 For any two vertices A and B:
  1. The fact that A can communicate with B implies that B can communicate with A
  2. There can be more than one edge between A and B.
  3. A can always communicate with B, although not necessarily directly.
  4. The associated matrix is symmetric; that is aij = aji for all possible values of i and j.

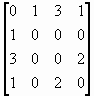
   Figure 9 shows the possible routes of communication between cities A, B, C, and D. Since communication is two-way, no arrowheads are needed. The associated matrix M for the digraph in Figure 9 is
A B C D
A
B
C
D
   Just as in the last section, the matrix M2 gives the number of communication routes between two cities that go through exactly one other city. Matrix M2 is
M2 = =

   The entry 3 in the fourth row of M2 shows that there are 3 routes connecting C and D that pass through exactly one other city (in this case, all three routes go through A). The entry 5 in the fourth row shows that there are 5 routes connecting city D with itself that go through exactly one other city. (One of these 5 routes goes through city A; the other four go through C.)
   As before, the matrix M3 would give the number of routes that pass through exactly two other cities. Also, the sum M + M2 gives the number of routes that pass through no cities or one city.

Organizational Communication   In some communication networks any two members can communicate directly. This is not always the case with organizational communication digraphs, however. (Mailroom clerks at Exxon probably don't chat with the chairman of the board, for example.) Assuming that only one method of communication exists between members of an organization, an organizational communication digraph has the following properties.
ORGANIZATIONAL COMMUNICATION
 For any two vertices A and B:
  1. If A communicates with B, then B communicates with A.
  2. No more than one edge connects A and B.
  3. A does not communicate with A.
  4. The associated matrix is a symmetric adjacency matrix.
   A typical organizational digraph is shown in Figure 10. The associated matrix for this figure is
A B C D E
A
B
C
D
E
   While A and E do not communicate directly in the digraph of Figure 10, they can communicate by going through B as an intermediary; alternate communication routes between A and E go through D, or through C and then B, among others. A route from one person to another, perhaps through intermediaries, is a path.
PATH
 A collection of vertices and edges leading from one vertex to another, with no vertex repeated, is called a path. If a path exists between each pair of vertices, the digraph is connected.

EXAMPLE 1
Use the organizational communication digraph in Figure 11 to answer the following questions.
(a) What are two possible paths from A to D?
   Two possible paths from A to D are shown in Figure 12. Note that a route that "doubles back," such as going from A to E are repeated.
(b) Is this digraph connected?
   There is a path connecting each pair of vertices, so the digraph is connected.
(c) What is the matrix for the digraph in Figure 11?
   The associated matrix for the digraph follows.
A B C D E
A
B
C
D
E
   We found by inspection that the digraph in Example 2 was connected. This process works well for most simple digraphs, but it is impractical for large ones. For larger digraphs, the following theorem (which we do not prove) is used.
THEOREM
 To decide whether an organizational communication digraph with n vertices is connected, first find the associated adjacency matrix M, and then form the sum
M + M2 + M3 . . . + Mn-1.
The digraph is connected if the matrix sum has only positive entries.


EXAMPLE 2
   Use the theorem to decide whether the following digraphs in Figure 13 are connected.
 
  (a) For Figure 13(a), first write the associated adjacency matrix M.
 
P Q R S
P
Q
R
S
     Since the digraph involves four vertices, the first 4 - 1 = 3 powers of M must be found. Calculation of M2 and M3 leads to the sum
 
Insert table of matrices
M + M2 + M3 = + + =
  All the entries in this matrix are positive, showing that the given digraph is connected.
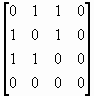
  (b) For Figure 13(b), the associated matrix M is
 
A B C D
A
B
C
D
  The sum M + M2 + M3 is
 
M + M2 + M3 = + + =
  The final matrix does not have all positive entries (some entries are 0), so the digraph is not connected. Insert end of exercise icon.

Exercises

Write the associated matrix for each digraph. Identify any communication digraphs or organizational communication digraphs
1. 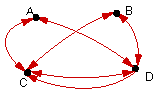2. 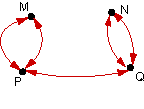3. 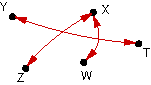4.
5. 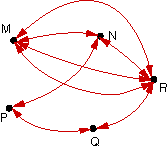6. 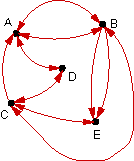7. 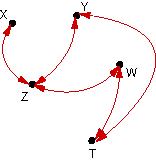8.
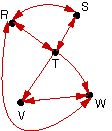Sketch a digraph for each matrix of a communication digraph in Exercises 9-16. Find all two-stage paths of communication.
9. 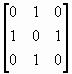10. 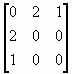11. 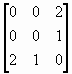12.
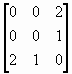13. 14. 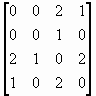15. 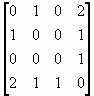16.
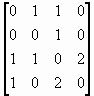Identify all paths from A to D in the following organizational communication digraphs.
17. 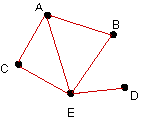18. 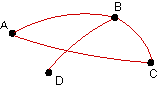19. 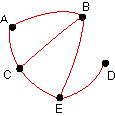20.
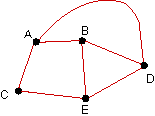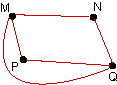
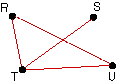
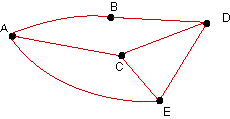
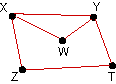
Use the theorem given at the end of the section to show that the following organizational communication digraphs are connected.
21. 22.
23. 24.
Show that the following organizational communication digraphs are not connected.
25. 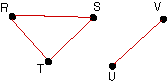26.

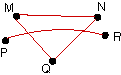Copyright © 1995-2012, Pearson Education, Inc.